2394: 1713A. Traveling Salesman Problem
Description
【题目大意】给出n个点,这些点要么位于x轴,要么位于y轴,请问从原点(0,0)出发,经过所有这n个点,并回到原点的最短距离是多少?
You are living on an infinite plane with the Cartesian coordinate system on it. In one move you can go to any of the four adjacent points (left, right, up, down).
More formally, if you are standing at the point (x,y)(x,y), you can:
- go left, and move to (x−1,y)(x−1,y), or
- go right, and move to (x+1,y)(x+1,y), or
- go up, and move to (x,y+1)(x,y+1), or
- go down, and move to (x,y−1)(x,y−1).
There are nn boxes on this plane. The ii-th box has coordinates (xi,yi)(xi,yi). It is guaranteed that the boxes are either on the xx-axis or the yy-axis. That is, either xi=0xi=0 or yi=0yi=0.
You can collect a box if you and the box are at the same point. Find the minimum number of moves you have to perform to collect all of these boxes if you have to start and finish at the point (0,0)(0,0).
The first line contains a single integer tt (1≤t≤1001≤t≤100) — the number of test cases.
The first line of each test case contains a single integer nn (1≤n≤1001≤n≤100) — the number of boxes.
The ii-th line of the following nn lines contains two integers xixi and yiyi (−100≤xi,yi≤100−100≤xi,yi≤100) — the coordinate of the ii-th box. It is guaranteed that either xi=0xi=0 or yi=0yi=0.
Do note that the sum of nn over all test cases is not bounded.
For each test case output a single integer — the minimum number of moves required.
Sample Input Copy
3
4
0 -2
1 0
-1 0
0 2
3
0 2
-3 0
0 -1
1
0 0
Sample Output Copy
12
12
0
HINT
In the first test case, a possible sequence of moves that uses the minimum number of moves required is shown below.
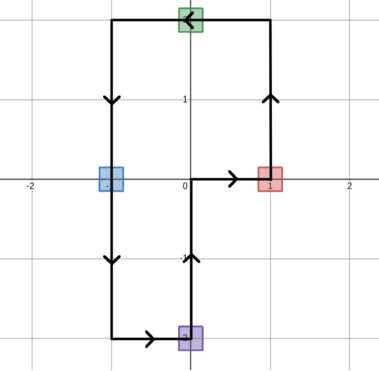
In the second test case, a possible sequence of moves that uses the minimum number of moves required is shown below.
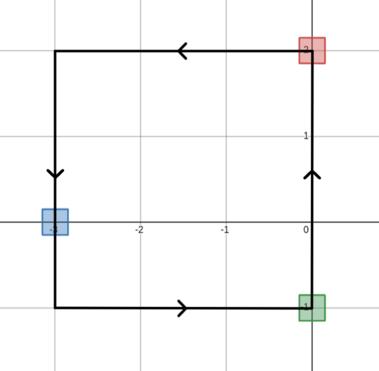
In the third test case, we can collect all boxes without making any moves.