3304: 【Div2】Happy new year 2025(5) - 蛇形行走
[Creator : ]
Description
给定一个有H行W列的方格。用(i, j)表示从上往下数第i行、从左往右数第j列的单元格。
每个单元格属于以下几种类型之一:
起点单元格、终点单元格、空白单元格或者障碍单元格。
这些信息由H个长度均为W的字符串S₁、S₂、…、Sₙ来描述。
具体而言,如果Sᵢ的第j个字符是“S”,那么单元格(i, j)就是起点单元格;
如果是“G”,则为终点单元格;
如果是“.”,就是空白单元格;
如果是“#”,就是障碍单元格。
可以保证恰好有一个起点单元格和一个终点单元格。 你当前位于起点单元格。你的目标是通过反复移动到与所在单元格有边相邻的单元格来抵达终点单元格。然而,你不能移动到障碍单元格上,也不能移动到方格之外,并且每次移动必须在垂直移动和水平移动之间交替进行(第一次移动的方向可以任意选择)。
判断是否有可能抵达终点单元格。如果可以,求出所需的最少移动次数。
更正式地说,检查是否存在一个单元格序列(i₁, j₁)、(i₂, j₂)、…、(iₖ, jₖ)满足以下所有条件,如果存在这样的序列,求出k - 1的最小值。
对于每一个1 ≤ l ≤ k,都有1 ≤ iₗ ≤ H且1 ≤ jₗ ≤ W,并且(iₗ, jₗ)不是障碍单元格。
(i₁, j₁)是起点单元格。 (iₖ, jₖ)是终点单元格。
对于每一个1 ≤ l ≤ k - 1,有|iₗ - iₗ₊₁| + |jₗ - jₗ₊₁| = 1。
对于每一个1 ≤ l ≤ k - 2,如果iₗ ≠ iₗ₊₁,那么iₗ₊₁ = iₗ₊₂。
对于每一个1 ≤ l ≤ k - 2,如果jₗ ≠ jₗ₊₁,那么jₗ₊₁ = jₗ₊₂。
约束条件:
1 ≤ H, W ≤ 1000 H和W是整数。
每个Sᵢ是一个由“S”、“G”、“.”、“#”组成的长度为W的字符串。
恰好有一个起点单元格和一个终点单元格。
每个单元格属于以下几种类型之一:
起点单元格、终点单元格、空白单元格或者障碍单元格。
这些信息由H个长度均为W的字符串S₁、S₂、…、Sₙ来描述。
具体而言,如果Sᵢ的第j个字符是“S”,那么单元格(i, j)就是起点单元格;
如果是“G”,则为终点单元格;
如果是“.”,就是空白单元格;
如果是“#”,就是障碍单元格。
可以保证恰好有一个起点单元格和一个终点单元格。 你当前位于起点单元格。你的目标是通过反复移动到与所在单元格有边相邻的单元格来抵达终点单元格。然而,你不能移动到障碍单元格上,也不能移动到方格之外,并且每次移动必须在垂直移动和水平移动之间交替进行(第一次移动的方向可以任意选择)。
判断是否有可能抵达终点单元格。如果可以,求出所需的最少移动次数。
更正式地说,检查是否存在一个单元格序列(i₁, j₁)、(i₂, j₂)、…、(iₖ, jₖ)满足以下所有条件,如果存在这样的序列,求出k - 1的最小值。
对于每一个1 ≤ l ≤ k,都有1 ≤ iₗ ≤ H且1 ≤ jₗ ≤ W,并且(iₗ, jₗ)不是障碍单元格。
(i₁, j₁)是起点单元格。 (iₖ, jₖ)是终点单元格。
对于每一个1 ≤ l ≤ k - 1,有|iₗ - iₗ₊₁| + |jₗ - jₗ₊₁| = 1。
对于每一个1 ≤ l ≤ k - 2,如果iₗ ≠ iₗ₊₁,那么iₗ₊₁ = iₗ₊₂。
对于每一个1 ≤ l ≤ k - 2,如果jₗ ≠ jₗ₊₁,那么jₗ₊₁ = jₗ₊₂。
约束条件:
1 ≤ H, W ≤ 1000 H和W是整数。
每个Sᵢ是一个由“S”、“G”、“.”、“#”组成的长度为W的字符串。
恰好有一个起点单元格和一个终点单元格。
Sample Input Copy
3 5
.S#.G
.....
.#...
Sample Output Copy
7
HINT
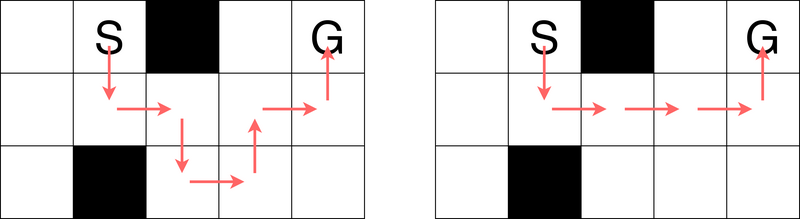
如左图所示,你可以按(1, 2)→(2, 2)→(2, 3)→(3, 3)→(3, 4)→(2, 4)→(2, 5)→(1, 5)这样的路径移动,通过7次移动抵达终点单元格。在6次或更少的移动次数内是无法做到的,所以答案是7。 请注意,你不能像右图所示那样,不交替地连续进行水平(或垂直)移动来选择路径。